الگوریتم دایجسترا،کاربردها و سورس برنامه

الگوریتم دایجسترا همراه توضیحات و پیچیدگی زمانی

در نظریه گراف، الگوریتم دیکسترا (به انگلیسی: Dijkstra’s algorithm)‏ یکی از الگوریتم‌های پیمایش گراف است که توسط دانشمند هلندی علوم رایانه، اِدْسْخِر دِیْکْسْترا در سال ۱۹۵۹ ارایه شد.

روند الگوریتم دیکسترا مطابق زیر می باشد :

۱- انتخاب راس مبدا

۲- مجموعه ی S ، شامل رئوس گراف ، معین می شود. در شروع، این مجموعه تهی بوده و با پیشرفت الگوریتم، این مجموعه رئوسی که کوتاه ترین مسیر به آن ها یافت شده است را در بر می گیرد.

۳- راس مبدا با اندیس صفر را در داخل S قرار می دهد.

۴- برای رئوس خارج از S ، اندیسی معادل ، طول یال + اندیس راس قبلی ، در نظر می گیرد . اگر راس خارج از مجموعه دارای اندیس باشد، اندیس جدید کمترین مقدار از بین اندیس قبلی و طول یال + اندیس راس قبل ، می باشد.

۵- از رئوس خارج مجموعه، راسی با کمترین اندیس انتخاب شده و به مجموعه ی S اضافه می گردد.

۶- این کار را دوباره از مرحله ی ۴ ادامه داده تا راس مقصد وارد مجموعه ی S شود.

در پایان اگر راس مقصد دارای اندیس باشد، اندیس آن نشان دهنده ی مسافت بین مبدا و مقصد می باشد. در غیر این صورت هیچ مسیری بین مبدا و مقصد موجود نمی‌باشد.

همچنین برای پیدا کردن مسیر می توان اندیس دیگری برای هر راس در نظر گرفت که نشان دهنده ی راس قبلی در مسیر طی شده باشد. بدین ترتیب پس از پایان اجرای الگوریتم، با دنبال کردن رئوس قبلی از مقصد به مبدا، کوتاه ترین مسیر بین دو نقطه نیز یافت می شود.

ر حین اجرای الگوریتم دو چیز به طور ضمنی نگهداری می‌شود. یکی مجموعهٔ از رأس‌هایی که وزن کوتاه‌ترین مسیر از مبدأ تا آن‌ها مشخص شده و دیگری دنبالهٔ که برای هر رأس ، مقدار برابر وزن کوتاه‌ترین مسیر از مبدأ تا است به شرطی که تمام رأس‌های این مسیر به جز از رئوس داخل باشند. در ابتدا تهی و مقادیر برای همهٔ رئوس به غیر از مبدأ بی‌نهایت است و مقدار آن برای مبدأ صفر گذاشته می‌شود. الگوریتم در هر مرحله رأسی خارج را که برای آن کمترین است انتخاب و به مجموعهٔ اضافه می‌کند و سپس مقادیر را برای رئوس همسایهٔ آن رأس به‌روز می‌نماید. در صورتی که نیاز به تشکیل درخت کوتاه‌ترین مسیر باشد، الگوریتم می‌بایست دنبالهٔ را که پدر رأس در درخت کوتاه‌ترین مسیر است، به همراه دنبالهٔ به‌روز کند.

پیچیدگی زمانی

در ساده‌ترین پیاده‌سازی الگوریتمِ دیکسترا، داده‌ها در آرایه یا لیست پیوندی ذخیره می‌شوند که بدین ترتیب مینیمم مقدار برای رئوس خارج با الگوریتمی خطی یافت می‌شود. در این حالت پیچیدگی زمانی خواهد بود، چراکه در گراف بدون جهت هر یال دقیقاً دوبار و در گراف جهت‌دار هر یال دقیقاً یک بار پیمایش می‌شود و هم‌چنین پیدا کردن مینیمم، زمان می‌خواهد که این مینیمم پیدا کردن بار تکرار خواهد شد. برای گراف‌های پراکنده (یعنی گراف‌هایی که خیلی کمتر از مجذور یال دارند) الگوریتم دیکسترا با نگهداری گراف در فهرست مجاورت و استفاده از صف اولویت‌دار (Priority-Queue) (برای پیدا کردن مینیمم) با پیچیدگی زمانی پیاده‌سازی می‌شود. در صورت استفاده از نگهدارندهٔ فیبوناتچی (Fibonacci heap) به جای صف اولویت‌دار، پیچیدگی زمانی با تحلیل جمعی (Amortized analysis) به 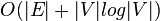بهبود می‌یابد.

کاربردها

ز جمله مهمترین کاربرد های این روش می توان به محاسبه ی کوتاه ترین فاصله ی دو نقطه در یک شهر از طریق راه های زمینی اشاره نمود. برای محاسبه ی کوتاه ترین مسیر بین دو نقطه باید نقاط مورد نظر در یک نقشه را علامت گذاری کرد و با استفاده از مشخصات نقاط(طول، عرض و ارتفاع) فاصله ی دو نقطه را در هر بار عملیات محاسبه نمود.توجه داریم که در ترافیک سرعت خودرو ها به شدت پایین آمده و این امر می تواند در انتخاب کوتاه ترین مسیر تاثیر گذار باشد چرا که ممکن است بین دو نقطه a,b راه های ۱و۲ موجود باشد که راه ۱ اتوبان و از خارج شهر و راه ۲ از داخل شهر عبور می کند. فرض کنید فاصله ی a,b از طریق راه ۱ حدود ۱۰ کیلومتر و از طریق راه ۲ حدود ۷ کیلومتر باشد ولی راه ۲ علی رقم فاصله ی کمتر دارای ترافیک سنگین است در نتیجه می توان انتظار داشت که در ساعات شلوغی استفاده از راه ۱ بهتر باشد.از آن جا که اساس محاسبات در این روش بر پایه ی فاصله بین دو نقطه است می توان کاهش سرعت را با افزایش فواصل هم ارز نمود چرا که اگر رابطه ی سرعت و فاصله را خطی در نظر بگیریم (D=V.T)تاثیر کاهش سرعت و افزایش مسافت یکسان است.از این رو لازم است تا ضرایب تعدیلی در فواصل بین نقاط ضرب شده و این مسائل را در محاسبات لحاظ کرد. از جمله مهم ترین این ضرایب می توان به ۳ مورد زیر اشاره نمود: ۱-ضریب ترافیک و شلوغی ۲-ضریب عرض معبر ۳-ضریب شیب که نشانگر افت سرعت در سر بالایی هااست. گرچه تعیین این ضرایب برای نقاط مختلف شهر نیازمند کارشناسان متخصص ترافیک و بررسی های آماری دقیق می باشد ولی می توان انتظار داشت که در اکثر موارد این ضرایب بین مقادیر ۱ تا ۲ بسته به شرایط تغییر کنند.

 

انواع روش ها والگوریتم های مسیریابی درشبکه اینترنت

الگوریتم مسیریابی ایستا :

هیچ اعتنایی به شرایط توپولوژیکی و ترافیک لحظه ای شبکه نمی شود و معمولاً هر مسیریاب برای هدایت بسته از جداولی استفاده می کند که در صورت وقوع هرگونه مشکل درزیر ساخت ارتباطی شبکه به صورت دستی تنظیم می گردند و در طول زمان ثابت می باشند که ترافیک لحظه ای هم به دلیل سریع بودن الگوریتم متغیر می باشد .

الگوریتم مسیریابی پویا :

مسیریابی براساس آخرین وضعییت توپولوژیکی و ترافیک شبکه انجام می شود و هرثانیه یکبار بروز می شوند،تصمیم گیری این الگوریتم براساس وضعییت فعلی شبکه می باشد ولی ممکن است به دلیل پیچیدگی بالای این الگوریتم زمان انتخاب بهترین مسیرطولانی شود و نهایتاً به ازدحام بینجامد که جهت رفع این مشکل از تکنیکهای چند پردازنده ای و پردازش موازی استفاده می گردد .

 الگوریتم متمرکز یا  :Link State

دراین الگوریتم هرمسیریاب باید5عمل زیر را انجام دهد:

1- آگاهی مسیریاب از اطلاعات کامل زیرساخت ارتباطی شبکه

2-شناسایی تمام مسیریابهای دیگر، ارتباطات بین آنها و هزینه ی هر خط توسط مسیریاب

3-جمع آوری اطلاعات کامل و تشکیل ساختمان داده ی مربوط به هرگراف زیرساخت ارتباطی

4-استفاده از الگوریتم کوتاهترین مسیر نظیر بهترین مسیر موجود بین دومسیریاب (دایجکسترا)

5-محاسبه مسیرهای جدید

1- شناسایی مسیریاب های مجاور :

با شروع به کار مسیریاب، اولین کاری که مسیریاب انجام می دهد شناسایی مسیریاب های مجاور با ارسال یک بسته ی خاص به نام بسته ی سلام یا Hello Packet  روی تمام خروجی های خود می باشد . مسیریاب ضمن پاسخ به این بسته آدرس جهانی خود را اعلام می نمایند و بعد از دریافت بسته های پاسخ ، این اطلاعات را در جدول خود درج می کنند .

2-اندازه گیری هزینه :

*  اندازه گیری تاخیر هریک از خطوط خروجی توسط هر مسیریاب با ارسال یک بسته ی  خاص با نام  Echo Packet بر روی تمام خطوط خروجی

*  پاسخ هر مسیریاب با بسته ی Echo Reply درصورت دریافت بسته ی Echo Packet

* در صورت پاسخ دهی به بسته ی  Echo یک زمان رفت و برگشت پیش می آید که تاخیر فیزیکی بین دو مسیریاب را به عنوان هزینه مشخص می کند که مسیریاب این زمان را با یک زمان سنج اندازه گیری نموده وبا تقسیم در جدولی درج می کند .

*  تشخیص مسیر بهینه همانند CF توسط مسیریاب ها و هدایت تمامی بسته ها از شبکه 1 و 2

*  تبدیل شدن مسیر CF به بدترین مسیر با گزارش تاخیر و ترافیک بالا در عرض چند ثانیه

*  انتخاب مسیر بهینه EI با داشتن ترافیک و تاخیر کمتر و هدایت بسته ها از این مسیر

*  تبدیل دوباره این مسیر به بدترین مسیر با گزارش تاخیر و ترافیک بالا در عرض چند ثانیه ی دیگر

*  تکرار روند نوسان تا بی نهایت

 

انواع روتر و کارکرد آنها

انواع روترها:
روترها را می توان به دو گروه عمده سخت افزاری و نرم افزاری تقسیم نمود:

روترهای سخت افزاری : سخت افزارهائی می باشند که نرم افزارهای خاص تولید شده توسط تولید کنندگان را اجراء می نمایند .نرم افزار فوق ، قابلیت روتینگ را برای روترها فراهم نموده تا آنان مهمترین و شاید ساده ترین وظیفه خود که ارسال داده از یک شبکه به شبکه دیگر است را بخوبی انجام دهند . اکثر شرکت ها ترجیح می دهند که از روترهای سخت افزاری استفاده نمایند چراکه آنان در مقایسه با روترهای نرم افزاری، دارای سرعت و اعتماد پذیری بیشتری می باشند .

روترهای نرم افزاری : روترهای نرم افزاری دارای عملکردی مشابه با روترهای سخت افزاری بوده و مسئولیت اصلی آنان نیز ارسال داده از یک شبکه به شبکه دیگر است. یک روتر نرم افزاری می تواند یک سرویس دهنده NT ، یک سرویس دهنده نت ور و یا یک سرویس دهنده لینوکس باشد . تمامی سیستم های عامل شبکه ای مطرح ،دارای قابلیت های روتینگ از قبل تعبیه شده می باشند . 
در اکثر موارد از روترها به عنوان فایروال و یا gateway اینترنت ، استفاده می گردد . در اکثر موارد نمی توان یک روتر نرم افزاری را جایگزین یک روتر سخت افزاری نمود ، چراکه روترهای سخت افزاری دارای سخت افزار لازم و از قبل تعبیه شده ای می باشند که به آنان امکان اتصال به یک لینک خاص WAN ( از نوع Frame Relay ، ISDN و یا ATM ) را خواهد داد .یک روتر نرم افزاری ( نظیر سرویس دهنده ویندوز ) دارای تعدادی کارت شبکه است که هر یک از آنان به یک شبکه LAN متصل شده و سایر اتصالات به شبکه های WAN از طریق روترهای سخت افزاری ، انجام خواهد شد .

مثال 1 : استفاده از روتر به منظور اتصال دو شبکه به یکدیگر و ارتباط به اینترنت 
فرض کنید از یک روتر به منظور اتصال دو شبکه LAN به یکدیگر و اینترنت ، استفاده شده است . زمانی که روتر داده ای را از طریق یک شبکه LAN و یا اینترنت دریافت می نماید ، پس از بررسی آدرس مبداء و مقصد ، داده دریافتی را برای هر یک از شبکه ها و یا اینترنت ارسال می نماید . روتر قادر است داده مورد نظر را به مقصد درست ، ارسال نماید . 

مثال 2: استفاده از روتر در یک شبکه LAN 
فرض کنید از یک روتر در یک شبکه LAN ، استفاده شده است . در مدل فوق ، هر یک از دستگاههای موجود در شبکه با روتر موجود نظیر یک gateway برخورد می نمایند . بدین ترتیب ، هر یک از ماشین های موجود بر روی شبکه LAN که قصد ارسال یک بسته اطلاعاتی ( اینترنت و یا هر محل خارج از شبکه LAN ) را داشته باشند ، بسته اطلاعاتی مورد نظر را برای gateway ارسال می نمایند . روتر ( gateway ) نسبت به محل ارسال داده دارای آگاهی لازم می باشد . ( در زمان تنظیم خصلت های پروتکل TCP/IP برای هر یک از ماشین های موجود در شبکه یک آدرس IP برای gateway در نظر گرفته می شود ) . 

مثال 3: استفاده از روتر به منظور اتصال دو دفتر کار 
فرض کنید ، بخواهیم از روتر به منظور اتصال دو دفتر کار یک سازمان به یکدیگر ، استفاده نمائیم . بدین منظور هر یک از روترهای موجود در شبکه با استفاده از یک پروتکل WAN نظیر ISDN به یکدیگر متصل می گردند . با استفاده از یک کابل که توسط ISP مربوطه ارائه می گردد ، امکان اتصال به اینترفیس WAN روتر فراهم شده و از آنجا سیگنال مستقیما" به شبکه ISP مربوطه رفته و سر دیگر آن به اینترفیس WAN روتر دیگر متصل می گردد . روترها ، قادر به حمایت از پروتکل های WAN متعددی نظیر Frame Relay , ATM , HDLC و یا PPP ، می باشند.

مهمترین ویژگی های یک روتر :
روترها دستگاههای لایه سوم ( مدل مرجع OSI ) می باشند . 
اکثر روترهای مهم دارای سیستم عامل اختصاصی خاص خود می باشند . 
روترها از پروتکل های خاصی به منظور مبادله اطلاعات ضروری خود ( منظور داده نیست ) ، استفاده می نمایند . 
آشنائی با اینترفیس های روتر :
همانگونه که در مطلب آشنایی با عناصر داخلی روتر اشاره گردید ، اینترفیس ها مسئولیت اتصالات روتر به دنیای خارج را برعهده داشته و می توان آنان را به سه گروه عمده اینترفیس های مختص شبکه محلی ، اینترفیس های مختص شبکه WAN و اینترفیس های کنسول و کمکی تقسیم نمود . 
انواع اینترفیس های روتر 
اینترفیس ها مسئولیت اتصالات روتر به دنیای خارج را برعهده داشته و می توان آنان را به سه گروه عمده تقسیم نمود :

اینترفیس های مختص شبکه محلی :
با استفاده از این اینترفیس یک روتر می تواند به محیط انتقال شبکه محلی متصل گردد. اینگونه اینترفیس ها معمولا" نوع خاصی از اترنت می باشند . در برخی موارد ممکن است از سایر تکنولوژی های LAN نظیر Token Ring و یا* ATM ( برگرفته از Asynchronous Transfer Mode ) نیز استفاده گردد.

ATM:
حالت انتقال ناهمگام (آسنکرون) یا ATM که مخفف Asynchronous Transfer Mode میباشد به پالسهای ساعت وابستگی نداشته و در رده شبکههای اتصال گرا تقسیم بندی میشود. در این مدل جهت برقراری اتصال در آغاز بستهای به سوی مقصد ارسال میشود، این بسته مسیر خود را بین مسیریابهای مختلف پیدا کرده و مدار مجازی را تشکیل میدهد. این اتصال که از این به بعد آنرا میتوان اتصال فیزیکی در نظر گرفت. هر یک از این اتصالها دارای یک شماره شناسایی است.
در این مدل اطلاعات به صورت بستههای ۵۳ بایتی(سلول) ارسال میگردد. این بستهها از دو بخش سرآیند و دادههای کاربر تشکیل شدهاند. در بخش سرایند که ۵ بایت است اطلاعاتی همچون شماره شناسایی اتصال ذخیره میگردد. ATMها سرعت بالایی دارند، بستهها را در یک مسیر و به ترتیب ارسال میکنند و از آنجایی که بستهها کوچک اند، کیفیت هم بالا است. این مدل شباهتهایی به شبکههای گسترده دارد و دارای پهنای باندی حدود ۶۲۲-Mbps است.

اینترفیس های مختص شبکه WAN :
این نوع اینترفیس ها اتصالات مورد نیاز از طریق یک ارائه دهنده سرویس به یک سایت خاص و یا اینترنت را فراهم می نمایند . اتصالات فوق ممکن است از نوع سریال و یا هر تعداد دیگر از اینترفیس های WAN باشند . در زمان استفاده از برخی اینترفیس های WAN ، به یک دستگاه خارجی نظیر CSU به منظور اتصال روتر به اتصال محلی ارائه دهنده سرویس نیاز می باشد . در برخی دیگر از اتصالات WAN ، ممکن است روتر مستقیما" به ارائه دهنده سرویس متصل گردد .

زیرشبکه

زیرشبکه

زیر شبکه (به انگلیسی: subnetwork)، زیرشاخه‌ای مشهود از یک IP شبکه است. به شیوه تقسیم یک شبکه به دو یا چند شبکه دیگر زیرشبکه‌بندی (به انگلیسی: Subnetting) می‌گویند.

عملیات زیرشبکه‌بندی به زبان ساده

همهٔ رایانه‌های متعلق به یک زیرشبکه با یک نگاشت بیت  مشترک و مشخص در آدرس IP داده می‌شوند که باعث می‌شود آدرس IP در طی یک تقسیم معقول به دو ناحیه تبدیل گردد که شامل یک شبکه یا پیشوند مسیریابی  و بخش دیگر یا شناسه میزبان  می‌باشد که این بخش یک شناسه برای میزبان مخصوص یا رابط شبکه است.

پیشوند مسیریابی در تعریف می‌شود که به عنوان بخش اول آدرس در شبکه نوشته می‌شود، در ادامه با یک (/) جدا شده و در انتها با طول بیت پیشوند آورده می‌شود.

برای نمونه: ۱۹۲.۱۶۸.۱.۰/۲۴ پیشوند نسخه ۴ پروتکل اینترنت  که در شروع شبکه در آدرس داده شده است، دارای ۲۴ بیت مختص است؛ و ۸ بیت باقی‌مانده برای آدرس دادن میزبان  ذخیره می‌شود. مشخصات آدرس IPv6 2001:db8::/32 با ۲۹۶ آدرس و یک پیشوند مسیریابی ۳۲ بیتی، یک بلوک آدرس بزرگ است. برای IPv4، یک شبکه با ماسک زیرشبکه  خودش هم متمایز و شناسایی می‌شود. ماسک زیرشبکه بیت‌مپ  است، هنگامی که توسط یک عملیات AND منطقی برای هر آدرس آی‌پی در شبکه به کار گرفته می‌شود محصولش یک پیشوند مسیریابی ست. ماسک‌های زیرشبکه همانند یک آدرس، در نشانه گذاری نقطه و اعشار  نیز تعریف می‌شوند. برای مثال: ۲۵۵.۲۵۵.۲۵۵.۰ یک ماسک شبکه برای پیشوند ۱۹۲.۱۶۸.۱.۰/۲۴ است.

هنگامی که پیشوندهای مسیریابیِ  آدرس منبع و آدرس مقصد با هم متفاوت باشند، ترافیک بین زیرشبکه‌ها با دروازه‌های  ویژه جابه‌جا می‌شود. یک رهیاب  مرزهای معقول و فیزیکی بین زیرشبکه‌ها را ایجاد می‌نماید.

فواید زیرشبکه‌بندی هر شبکه موجود با هر طرح مستقر متفاوت است. در یک طرح تخصیص آدرس از اینترنت با استفاده از CIDR و در یک ساختار بزرگ، اختصاص فضای کافی برای آدرس لازم و ضروری‌ست. این طرح ممکن است کارآیی مسیریابی را افزایش بدهد، و یا هنگامی که زیرشبکه‌ها توسط اشخاص مختلف در یک ساختار بزرگ‌تر به صورت اداری کنترل می‌شوند، در مدیریت شبکه مزایایی داشته باشد. احتمال دارد زیرشبکه‌ها در یک معماری سلسله وار و منطقی مرتب شده باشند. بخش‌بندی فضای آدرس، شبکهٔ سازمان را به یک ساختار درخت مانند مسیریابی بدل می‌کند.

آدرس‌دهی و مسیریابی شبکه

رایانه‌هایی که در یک شبکه همانند اینترنت حضور دارند هر یک حداقل دارای یک آدرس منطقی هستند. معمولاً هر وسیله دارای یک آدرس مختص به خود است که می‌تواند توسط سرور یک شبکه به طور خودکار با یک قرارداد پیکربندی پویای میزبان  سازمان‌دهی شود. که به صورت دستی توسط یک مجری و به صورت خودکار توسط stateless address auto configuration انجام می‌شود. یک آدرس وظیفه شناسایی میزبان و مکان آن در شبکه را داراست. رایج ترین معماری آدرس شبکه، پروتکل اینترنت نسخه ۴ است، امّا استفاده از جانشین آن یعنی IPv6 دقیقاً از سال ۲۰۰۶ به صورت چشم‌گیری گسترش یافته است. آدرس IPv4 متشکل از ۳۲ بیت، برای خوانایی در یک فرم متشکل از ۴ رقم اعشار آکتت و جدا شده با نقطه‌ها نوشته می‌شود که به این سیستم، نشانه‌گذاری نقطه و اعشار dot-decimal notation گفته می‌شود. آدرس IPv6 IPv6 address متشکل از ۱۲۸ بیت در یک نشانه گذاری بر مبنای ۱۶ و گروه‌بندی ۱۶ بیتی و جدا شده با دونقطه (:) نوشته می‌شود. به منظور مدیریت شبکه، آدرس IP به دو بخش منطقی تقسیم می‌شود به نام‌های: پیشوند شبکه و شناسه میزبان یا " بخش دیگر". همهٔ میزبان‌های روی یک زیرشبکه دارای پیشوند شبکه یکسان می‌باشند. این پیشوند مسیریابی قابل توجه ترین بیت آدرس را اشغال می‌کند. میزان بیت تخصیص داده شده درون یک شبکه برای یک پیشوند مسیریابی داخلی، بسته به معماری شبکه ممکن است بین زیرشبکه‌ها متفاوت باشد. هنگامی که در IPv6 یک پیشوند باید شامل مجموعه‌ای از بیت‌های یک هم‌جوار باشد، این در IPv4 اجباری نیست. استفاده از بیت‌های یک غیر هم‌جوار فایده‌ای نیز ندارد. بخش میزبان، یک شناسایی خاص محلی است و همین طور یک شماره میزبان روی شبکهٔ محلی و یا شناسه رابط است.

این ساختار آدرس‌دهی منطقی به مسیریابی گزینشی اجازه می‌دهد که اگر پیشوندهای شبکه مبدأ و مقصد با میزبان‌ها متفاوت باشند، از بسته‌های IP از میان شبکه‌های چندگانه توسط دروازه‌های مخصوص رایانه‌ها -که ره‌یاب نامیده می‌شود- به میزبان هدف گذر کنند، و اگر آن‌ها یکسان باشند مستقیماً به میزبان هدف روی شبکهٔ محلی فرستاده می‌شود. رهیاب‌ها از مرزهای منطقی و فیزیکی بین زیرشبکه‌ها متشکل می‌شوند و هم‌چنین ترافیک بین آن‌ها را مدیریت می‌کنند. هر زیرشبکه توسط یک ره‌یاب پیش‌فرض تعیین شده، سرویس داده می‌شود. اما احتمال دارد که به صورت داخلی شامل Ethernet چندگانه فیزیکی، با قسمت‌های مرتبط به هم توسط کلیدها و یا پل‌های شبکه network switches یا network bridges. باشد. پیشوند مسیریابی یک آدرس در یک فرم مشابه به آدرس خودش نوشته می‌شود که این ماسک شبکه یا ماسک زیر شبکه آدرس نامیده می‌شود. به طور مثال، یک مشخصه از چشم‌گیرترین آدرس ۱۸ بیتی IPv4 11111111.11111111.11000000.00000000 به صورت ۲۵۵٫۲۵۵٫۱۹۲٫۰ نوشته می‌شود. اگر این ماسک به یک زیرشبکه درون یک شبکه بزرگ‌تر تخصیص داده شود به آن ماسک زیر شبکه نیز می‌گویند. هرچند این نوع از علامت گذاری ماسک شبکه فقط برای شبکه‌های IPv4 استفاده می‌شود.

نوع پیشرفته و استاندارد برای تخصیص پیشوند شبکه، نشانه گذاری CIDR CIDR notation است که برای هر دو IPv4 و IPv6 استفاده می‌شود. در این روش تعداد بیت‌های یک پیشوند شمرده می‌شود و این عدد پس از یک علامت اسلش جدا کننده (/) به آدرس اضافه می‌شود:

• ۱۹۲.۱۶۸.۰.۰، ماسک شبکه ۲۵۵.۲۵۵.۲۵۵.۰ که به صورت ۱۹۲.۱۶۸.۰.۰/۲۴ نوشته می‌شود.
• در IPv6، 2001:db8::/۳۲ آدرس 2001:db8:: را تخصیص می‌دهد و پیشوند شبکه اش شامل مهم ترین ۳۲ بیت می‌شود.

این نشانه گذاری با سی‌آی‌دی‌آر در RFC 4632معرفی شد. در IPv6، این تنها نوع علامت گذاری قابل قبول شبکه یا پیشوند مسیریابی‌ست.

در classful networking، در IPv4، مقدم بر معرفی CIDR، می‌شود پیشوند شبکه را مستقیماً بر اساس بالاترین بیت در توالی اش از آدرس IP به دست آورد. از این طریق ابتدا کلاس آدرس (A, B, C) و در ادامه ماسک شبکه مشخص می‌شود. از هنگام معرفی CIDR، تخصیص یک آدرس IP به یک رابط شبکه، نیازمند دو پارامتر آدرس و ماسک شبکه اش است.

در IPv4، هنگامی که یک آدرس نتواند از یک پیشوند روی لینک قطع رابطه کند، به سادگی یک لینک معین برای آدرس IP، توسط آدرس و وضعیت ماسک شبکه داده می‌شود. ولی برای IPv6، این لینک معین در جزئیات متفاوت است و به ان‌دی‌پی احتیاج دارد. تخصیص آدرس IPv6 به یک رابط -به استثناء آدرس‌های محلی لینک- احتیاجی به هماهنگی با پیشوند روی لینک ندارد.

در حالی که زیرشبکه‌بندی ممکن است کارآیی شبکه را در یک شبکهٔ سازمان یافته افزایش دهد، پیچیدگی مسیریابی را نیز بیشتر می‌کند، چون هر زیرشبکه محلی متصل، باید توسط یک ورودی جدا در جدول‌های مسیریابی routing tables مربوط به هر ره‌یاب متصل، نشان داده شود. در هر حال با یک طرح دقیق از شبکه، ره‌یاب‌ها می‌توانند به مجموعه‌ای از زیرشبکه‌های دورتر درون شاخه‌های یک درخت طبقه‌بندی شده اضافه شوند. قابلیت VLSM در ره‌یاب‌های تجاری، معرفی CIDR را در میان اینترنت و تشکیلات شبکه‌ها یکپارچه می‌سازد.

زیرشبکه بندی آی‌پی نسخه ۴

فرایند زیرشبکه‌بندی، فرایندی‌ست که شامل جداسازی شبکه و زیرشبکه آدرس از شناسه میزبان می‌شود. این فرایند توسط عملیات bitwise AND بین آدرس IP و ماسک زیرشبکه انجام می‌گیرد. نتیجه این فرایند آدرس شبکه و یا پیشوند است به علاوه یک باقی‌مانده که شناسه میزبان است.

تعیین پیشوند شبکه

یک ماسک شبکه IPv4، شامل ۳۲ بیت، یک توالی از یک‌ها (۱) به همراه یک بلوک (۰) می‌باشد. بلوک صفرها بخشی را به عنوان شناسه میزبان تخصیص می‌دهد. مثال زیر جدایی یک شناسه میزبان و پیشوند شبکه را از آدرس (۱۹۲.۱۶۸.۵.۱۳۰) نشان می‌دهد و به /۲۴ ماسک شبکه (۲۵۵.۲۵۵.۲۵۵.۰) مرتبط می‌شود. این عملیات در یک جدول به طریق آرایش binary نشان داده می‌شود.

عملیات ریاضی به منظور محاسبه پیشوند شبکه با bitwise AND آدرس IP و ماسک زیرشبکه است. نتیجه این عملیات منجر به پیشوند شبکه ۱۹۲.۱۶۸.۵.۰ و عدد میزبان ۱۳۰ می‌شود.

زیرشبکه‌بندی

زیرشبکه‌بندی فرایندی‌ست که بخشی از بیت‌های بالا مرتبه از قسمت معین میزبان با ماسک شبکه از ماسک زیرشبکه، گروه‌بندی می‌شوند. این عمل، شبکه را به زیرشبکه‌های کوچک‌تر تقسیم می‌کند. نمودار زیر، مثال را با حرکت دو بیت از بخش میزبان به ماسک زیرشبکه به شکل ۴ زیرشبکه کوچک‌تر که یک چهارم اندازه قبلی خود هستند، توصیف می‌کند.

	به صورت باینری	به صورت اعشار نقطه‌ای
نشانی آی‌پی	11000000.10101000.00000101.10000010	192.168.5.130
ماسک زیرشبکه	11111111.11111111.11111111.11000000	255.255.255.192
پیشوند شبکه	11000000.10101000.00000101.10000000	192.168.5.128
بخش هاست	00000000.00000000.00000000.00000010	0.0.0.2

 

وایمکس

وایمکس به انگلیسی: WiMAX) یا هم‌کُنش‌پذیری جهانی برای دسترسی ریزموج (به انگلیسی: WorldWide Interoperability for Microwave Access)، پروتکل ارتباطی برای دسترسی پهن باند بی‌سیم بر پایه استاندارد آی‌تریپل‌ئی ۸۰۲٫۱۶ است. وای‌مکس امکان دسترسی به اینترنت را به هردو صورت ثابت و کاملاً سیار در یک ناحیهٔ گسترده فراهم می آورد.(۲۰۱۰ میلادی )آخرین بازبینی وایمکس امکان دسترسی با نرخ انتقال داده ۴۰ مگابیت بر ثانیه را عرضه می کند. با استاندارد آی‌تریپل‌ئی ۸۰۲٫۱۶ انتظار می رود که سرعت انتقال تا یک گیگابیت بر ثانیه افزایش یابد.نام وایمکس توسط انجمن وایمکس انتخاب شد که در سال ۲۰۰۱ برای ارتقای همنوایی و همکنش پذیری این استاندارد تاسیس شد. این انجمن وایمکس را به عنوان یک فناوری برپایه استاندارد تعریف می کند که امکان دسترسی بی سیم پهن باند را به عنوان جایگزینی برای کابل و خطوط دی اس ال(DSL) ارائه می دهد.

واژه شناسی

منظور از واژه وایمکس پیاده سازیهای همکنش پذیر استاندارد آی‌تریپل‌ئی ۸۰۲٫۱۶ برای شبکه های بی سیم است (که به تصویب انجمن وایمکس رسیده است) واز این نظر به وای-فای شباهت دارد که شامل پیاده سازیهای همکنش پذیر استاندارد آی‌تریپل‌ئی ۸۰۲٫۱۱ می شود.

انجمن وایمکس گواهینامه هایی صادر می کند که به موجب آن فروشندگان می توانند محصولات خود را با گواهی وایمکس به فروش برسانند.بدین ترتیب محصولات فروشندگان مختلفی که گواهی وایمکس می گیرند اگر در یک پروفایل باشند می توانند با یکدیگر کارکنند و سطحی از همکنش پذیری پدید می آید.

استاندارد IEEE 802.16 پایه وایمکس است اگرچه گاهی به صورت محاوره ای از این استاندارد هم به عنوان وایمکس یاد می شود. از استاندارد IEEE 802.16d به نام وایمکس ثابت و از استاندارد IEEE 802.16e به نام وایمکس سیار یاد می شود.

ویژگی ها

برخی از مهمترین ویژگی‌های فناوری وایمکس به شرح زیر است:

نرخ انتقال داده بالا 

با استفاده از آنتن های مایمو (Multiple Input Multiple Output ) به همراه زیر-کانال سازی انعطاف پذیر و کدگذاری و مدولاسیون پیشرفته، فناوری وایمکس را قادر می سازد تا به سرعت بارگیری تا 63 مگابیت بر ثانیه و بارگذاری تا 25 مگابیت برثانیه دست یابد.

کیفیت سرویس (QoS) 

یکی از اصول معماری MAC در استاندارد IEEE 802.16 کیفیت سرویس است. این استاندارد جریانهای سرویسی را تعریف می کند که می تواند به نقاط کد(DSCP) در سرویسهای متمایز (DiffServ) و یا برچسب های جریان در MPLS نگاشته شوند.

امنیت 

ویژگیهای امنیتی وایمکس بر پایه پروتکل احراز هویت گسترش پذیر (EAP) و استاندارد رمزنگاری پیشرفته (AES) و پیامهای کنترلی CMAC و کد اصالت‌سنجی پیام برپایه درهم‌سازی بنا شده اند.

پوشش وسیع 

برجسته ترین ویژگی وایمکس پوشش گسترده آن نسبت به وای-فای است. در حال حاضر از لحاظ نظری وایمکس می تواند محدوده ای به شعاع 30 مایل( 50 کیلومتر) را پوشش دهد که اگرچه در عمل این مقدار به 10 کیلومتر می رسد، نسبت به فناوریهای پیشین خود (مانند وای-فای) جهشی نسبتاً بزرگ است.

سیار بودن 

دیگر ویژگی مهم وایمکس امکان اتصال در حین حرکت برای ایستگاههای سیار است.

ایستگاههای واسطه 

امواج رادیویی وایمکس از ایستگاه های پایه به سوی مشترکین ارسال می شوند.در این ایستگاهها سخت افزار هایی برای ارائهٔ وایمکس در یک ناحیه محدود نصب شده اند. از آنجا که هر ایستگاه پایه ناحیه محدودی را پوشش می دهد با اتصال این ایستگاهها به یکدیگر می توان ناحیه تحت پوشش را گسترش داد.

دسترسی 

اتصال به ایستگاههای پایه وایمکس به سادگی صورت می پذیرد و نیاز به دانش فنی ندارد.

مقیاس پذیری(Scalability)

فناوری وایمکس به گونه‌ای طراحی شده است که در محدوده کانالهای۲۰MHz تا ۱٫۲۵ قادر به کار کردن است. از نتایج این امر راحتی پیاده سازی شبکه با ایجاد تغییرات جزئی در قسمت Air Interfaceمی باشد و بسته به مدل مصرف بر اساس نوع سرویس و طیف فرکانسی آزاد، وایمکس قابل پیاده سازی در فرکانس های متفاوتی می‌باشد.این خصوصیت همچنین باعث می‌شود که محدوده کشورها بر اساس نیازمندیهای منطقه‌ای مختلفشان برای مثال نیاز به دسترسی به اینترنت در شهر و با دسترسی پرظرفیت باند وسیع متحرک در متروها و حومه شهر قادر، به استفاده موثر و چند منظوره‌ای از این فناوری باشند.

کاربردهای عملی وایمکس

پوشش وسیع و پهنای باند بالای وایمکس آن را برای کاربردهای زیر مناسب می سازد:

• امکان اتصال پهن باند بی سیم در میان شهرها و کشورها از طریق طیف متنوعی از دستگاهها
• ارائه جایگزینی برای دسترسی پهن باند دی اس ال و کابلی
• ارائه منبعی برای دسترسی به اینترنت برای بکارگیری در برنامه ریزی پیوستگی کسب و کار
• ارائه سرویسهای داده، مخابراتی(VOIP) و تلویزیون اینترنتی

پهن باند(Broadband)

شرکتهای متعددی در حال به کارگیری وایمکس برای ارائه اتصال پهن باند به هر دو صورت سیار و خانگی در سراسر نقاط شهرها و کشورهای مختلف هستند. در بسیاری از موارد این موضوع سبب بروز رقابت در بازار هایی که پیش از این تنها از فناوریهای دی اس ال و مشابه آن استفاده می کردند شده است.

علاوه بر این هزینه نسبتاً پایین پیاده سازی یک شبکه وایمکس (در مقایسه با جی‌اس‌ام، فیبرنوری و دی اس ال) امکان دسترسی پهن باند را در مناطقی که از لحاظ اقتصادی امکانپذیر نبوده اند را فراهم می سازد.

بک هال(Backhaul)

وایمکس می تواند جایگزینی برای فناوریهای تلفن همراه مانند جی اس ام(GSM) و سی دی ام ای(CDMA) باشد. وایمکس ثابت نیز به عنوان فناوری بک هال بی سیم برای شبکه های 3G, 2G و 4G در کشورهای توسعه یافته و در حال توسعه محسوب می گردد. با استفاده از وایمکس می توان اتصالهای نقطه به نقطه به طول 30 مایل(50 کیلومتر) و با نرخ انتقال داده ای که می تواند از چندین خط E1 و T1 پشتیبانی کند ایجاد کرد و بدین ترتیب از این فناوری برای اتصال ایستگاههای پایه به مراکز سوییچینگ استفاده نمود. ترافیک شبکه های تلفن همراه (سلولی) ترکیبی از صدا و داده است که ویژگی QoS ذاتی وایمکس برای این کاربرد بسیار مناسب است.

سرویس سه گانه(Triple-Play)

وایمکس با پشتیبانی از فناوریهایی چون کیفیت سرویس (QoS) و چندپخشی امکان ارایه سرویسهای سه گانه را فراهم می کند. از این رو اپراتور وایمکس می تواند علاوه بر دسترسی پهن باند سریع به اینترنت، سرویسهای VOIP و IPTV را نیز به مشتریان عرضه کند.

شبکه های بانکی

بانکهای بزرگ می توانند برای اتصال شعبه ها و دستگاههای خودپرداز به یکدیگر از شبکه های خصوصی وایمکس استفاده کنند. این بانکها معمولاً در نواحی وسیعی گسترده شده اند و نیاز به امنیت و پهنای باند بالا دارند که ویژگیهای ذاتی وایمکس این نیاز را برطرف می سازد.

علاوه بر این ها وایمکس می تواند در بسیاری از شبکه های خصوصی و عمومی دیگر مانند محوطه دانشگاهها، محیط های آموزشی، شبکه های ایمنی عمومی (مانند آتش نشانی و پلیس) نیز به کاررود.